2. Geometrie prostoru

 

2.1. Euklidovská geometrie, Euklidovský prostor

 

2.1.       Skutečnost, že jsme „malí mravenci“, žijící na obrovské kouli vyústila ve falešnou iluzi ploché Země. Na této představě vyrostla Euklidovská geometrie, která nás provází „od kolébky po hrob“. Jsme v ní (školou) vychovaní a neumíme si představit, že by se prostor mohl dělit nebo popisovat jinak. Domníváme se, že Euklidovská geometrie je univerzální (použitelná v celém Univerzu), že s ní lze popsat celý Vesmír a všechny jevy v něm. To je falešná iluze. [1]

2.2.       Euklidovský prostor je prostor virtuální (neskutečný, vymyšlený). Euklidovský prostor nevychází z přírodních sil a nemá žádné fyzikální vlastnosti (pokud je tam „nenadefinujeme“). Vytváří předpoklady pro falešnou iluzi jakéhosi neutrálního jeviště, kde se nacházejí „teoretická tělesa“ a odehrávají se „teoretické“ fyzikální děje. Je charakterizován pouze (lineárním) rozměrem. Umožňuje falešnou iluzi linearity, homogenity, symetrie, klidu a „vakua“. [2]

2.3.       Euklidovská geometrie představuje vnímání prostoru, vycházející z představy ploché Země. Je charakterizována soustavou tří kolmých dvourozměrných rovin, protínajících se v jednom „bodě“. Základní křivka v Euklidovském prostoru je lineární přímka, základní plocha je lineární rovina, základní těleso je (homogenní, [3] symetrická, statická, uzavřená) krychle. Mohou zde existovat uzavřené (rotující) křivky a uzavřené plochy. Euklidovské (2D) plochy nemají objem.

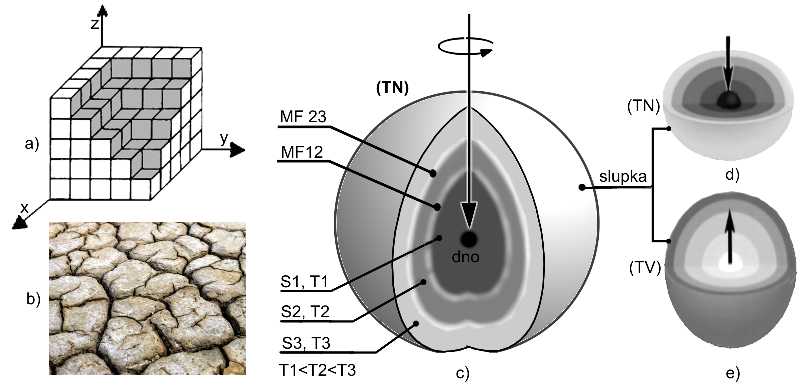
2.4.       Dělení Euklidovského prostoru nevychází z přírodních sil (Obr. 2.1. a). Euklidovský prostor se dělí podle (virtuálních) pravoúhlých lineárních os (x, y, z) do stejných (virtuálních) homogenních, statických krychliček, znázorněných stejnou šedou barvou. Polohu a objem každé krychličky lze přesně určit. Krychličky jsou uzavřená tělesa, mají společné (virtuální) plochy a není jasné, co je od sebe odděluje. Krychličky lze dělit na stále menší stejné, symetrické a homogenní celky.

2.5.       V mechanice a z ní vzešlé „fyzice“ pracující s falešnou iluzí lineárního (plochého, nespojitého) Euklidovského prostoru jsou tělesa od prostoru oddělená. Prostor není považován za (složené) těleso. Vlastnosti těles jsou nezávislé na jejich poloze v prostoru. Mohou zde být dvě (a více) těles se shodnými, statickými vlastnostmi. Tělesa jsou zdrojem „sil“, které z nich vystupují po celou dobu jejich existence (perpetuum mobile). Existují zde absurdity: prázdný prostor = „vakuum“ a absurdní těleso bez objemu a plochy = „hmotný bod“ a další.

 

2.6. Sférický prostor, sférická geometrie

 

2.6.       Sférický prostor je prostor fyzikální (skutečný, materiální). [4] Sférický prostor je fraktální systém fyzikálních hustot a fyzikálních tlaků. Sférický prostor se diferencuje pouze podle hustoty - jinou možnost nemá. Hustota prostoru a od ní v nepřímé úměrnosti odvozený tlak (teplota) jsou základní fyzikální parametry. Fyzikální hustota prostoru [5] je vždy kladné číslo. Fyzikální hustota prostoru je konečná (hustotní dno).

2.7.       Ve sférickém prostoru nelze nalézt dvě stejné oblasti, dvě stejná (shodná) tělesa, nebo dvě shodné trajektorie. Ve sférickém prostoru nelze nalézt dvě shodné, nebo shodně se opakující události. Sférický prostor je přísně materiální. Sférický prostor je neinerciální.

 

 

Obr. 2.1.

 

2.8.       Dělení sférického prostoru je přirozené (vychází z přírodních sil). Sférický prostor se skládá ze spojité jednoty částic s charakterem tlakových výší a tlakových níží. Na (Obr. 2.1. b) je vidět přirozené dělení sférického prostoru na příkladu rozpraskané půdy. Oblasti s vysokou hustotou prostoru (půda) jsou obklopeny oblastmi s nízkou hustotou prostoru (atmosféra) a zároveň oblasti s nízkou hustotou prostoru jsou obklopeny oblastmi s vysokou hustotou prostoru. Tyto přirozené (vláknité) materiální struktury se vyskytují v různých podobách ve všech vztažných soustavách Univerza (Obr. 4.2., Obr. 4.3.). Dělení takových přirozených sférických struktur podle Euklidovských pravoúhlých os, nebo rovin není možné.

2.9.       Sférický prostor se organizuje podle své hustoty. Proces sedimentace tlačí tělesa (prostorové anomálie) podle jejich hustoty prostoru do hustotních sfér, do kterých svojí hustotou prostoru patří. V prostoru vzniká systém otevřených nesymetrických sfér (vrstev) s rostoucí nebo klesající hustotou prostoru. V každé hustotní sféře je jiná hustota prostoru a od ní v nepřímé úměrnosti odvozený tlak.

2.10.    Vrstva, ve které mají tělesa podobnou hustotu prostoru, se nazývá fáze. Sousedící fáze jsou od sebe odděleny fyzikálními plochami, které se nazývají mezifází (z rozdílu hustot v prostoru vzniká plocha). Mezifází nejsou zcela ostrá a zřetelná. Mezifází nelze exaktně definovat. Čím je rozdíl v hustotě prostoru mezi dvěma fázemi větší, tím je mezifází mezi nimi užší. Čím je rozdíl v hustotě prostoru mezi fázemi menší, tím je mezifází mezi nimi širší a méně zřetelné. [6]

2.11.    Nehomogenní sférický prostor může nabývat dvou stavů. Tlaková níže - hustota prostoru roste (tlak klesá) po spirále směrem od slupky do centra (Obr. 2.1. c, d). Tlaková výše - hustota prostoru roste (tlak klesá) po spirále směrem od centra ke slupce (Obr. 2.1. e).

2.12.    Na (Obr. 2.1. c) je zjednodušené schematické znázornění sférického prostoru s charakterem tlakové níže (TN). Hustota prostoru směrem od slupky do středu roste, tlak klesá (T1 < T2 <T3). Procesem sedimentace vzniklé hustotní fáze (S1, S2, S3) od sebe oddělují mezifází (MF12, MF23...). Střed níže (TN) tvoří hustotní dno systému.

2.13.    Základní křivka (trajektorie) ve sférickém prostoru je fraktální spirála. Základní plocha ve sférickém prostoru je spirální toroid. [7] Základní těleso ve sférickém prostoru je nehomogenní, nesymetrická, dynamická částice. Částice je otevřené těleso, ohraničené spojitou množinou (otevřených) ploch spirálních toroidů. Částice je pouze složitá („zamotaná“) otevřená fraktální plocha.

 

2.14.    Fraktální sférická geometrie prostoru objasňuje, podle jakých pravidel se fyzikální prostor organizuje do hustotních sfér a podle jakých pravidel se jednoduchá tělesa (částice) spojují do větších nadřazených celků (složených těles). Případně jak se v nadřazených tlakových systémech utvářejí podřízené systémy. Vzhledem k fraktálnosti prostoru a všech těles v něm, je sférická geometrie schopná popsat všechny fyzikální jevy na všech velikostních úrovních prostoru, včetně složitých biologických systémů. Nejedná se o klasickou geometrii s „pravítkem a kružítkem“. [8] Sférická geometrie prostoru nemá žádný zobrazovací aparát. Při zobrazování dějů ve sférickém prostoru jsme odkázáni na Euklidovskou geometrii.

 

2.15. Vztahy mezi plochou a tělesem

 

2.15.    Povrchová plocha je nutnou podmínkou existence tělesa. Plocha tělesa je tlakový orgán. Plocha tělesa má dostřednou stranu (d), působící tlakem směrem do středu tělesa a odstřednou stranu (o) působící tlakem směrem od středu tělesa. Tlak z odstředné plochy tělesa se nazývá povrchový tlak. Je to tlak, kterým působí (vnější) plocha tělesa na vnější plochu jiného tělesa.

 

 

Obr. 2.2.

 

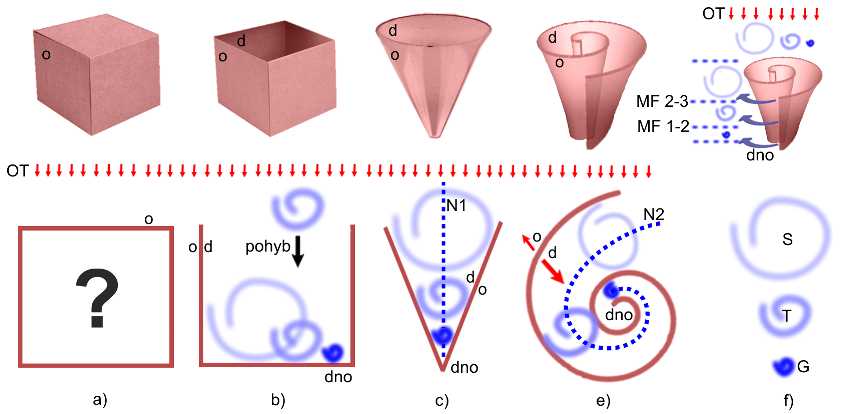
2.16.    Příklad. 2.1. Na (Obr. 2.2.) je naznačen vztah mezi několika typy (hmotných) těles (a, b, c, e) a jejich plochami. [9] Jsou zde rovněž tři „částice“ (S, T, G) s různou hustotou prostoru. Jejich povrchové plochy (slupky) jsou zjednodušeně znázorněné jako jednoduché neuzavřené spirály (Obr. 2.2. f).

2.17.    Hustotu prostoru částice určuje součet hustoty slupky a hustoty toho, co je pod vnitřní (dostřednou) stranou slupky. Částice (S) má velký objem, poměrně úzkou (hustou) slupku a velkou povrchovou plochu. Hustota prostoru částice (S) je velmi malá. To znamená, že uvnitř částice je velmi vysoký tlak (teplota). Částice (T) má objemnější (hustou) slupku, menší objem prostoru pod slupkou a menší povrchovou plochu. Uvnitř částice je nižší tlak (teplota) než je v (S). Hustota prostoru částice (G) je maximální, teplota dosahuje teplotního dna („nula“ stupňů K), její objem je minimální. [10] Nic hustšího (studenějšího) v prostoru nemůže existovat.

2.18.    Tělesa (a, b, c, e) i částice (S, T, G) se nacházející se v orientovaném tlakovém poli (OT), působícím „shora“ (dostředně). Orientovaný tlak (OT) působí na plochy částic (S, T, G) a důsledkem toho je jejich (dostředný) pohyb. Tělesa (a, b, c, e) se liší svými plochami.

2.19.    Plocha tělesa (a) je uzavřená. Uzavřené těleso má pouze odstřednou plochu (o). Do takového tělesa nelze nic vložit, ani z něho nic vyjmout. Tlak (OT) působí na povrchovou plochu tělesa (a) a může způsobit jeho pohyb.

2.20.    Plocha těles (b), (c) by se dala nazvat „polouzavřená“. Do těles (b), (c) mohou být částice (S, T, G) tlakem (OT) vtlačeny, ale nemohou z nich uniknout. Tlak (OT) na (horní) plochu částic je větší, než tlak (d) z ploch těles (b), (c) na (dolní) plochu částic. Částice (tělesa) nejsou zdrojem žádných sil a nemohou se z těles (b, c) samy dostat a zůstávají v tělesech (b, c).

2.21.    Mezi tělesy (b), (c) je rozdíl ve tvaru povrchové plochy. Těleso (c) má tvar kužele (sedimentační kužel). Tvar povrchové plochy tělesa (c) a tlak (d) z jeho plochy, neumožňuje částicím s velkým objemem (S) dostat se až na dno kužele. Tam se dostane pouze nejhustší částice (G), s nejmenším objemem a plochou. Dostředná plocha tělesa (c) „třídí“ částice podle hustoty. V „ose“ kužele (c) se vytvoří oblast snižujícího se tlaku (N1).

2.22.    Zužující se spirální plocha tělesa (e) je otevřená. Do tělesa (e) lze něco vložit (vtlačit) a také z něho může být něco vytlačeno. Částice (S, T, G) jsou tlačeny (OT) do tělesa (e). Hustota prostoru částic roste po spirále (N2) směrem ke dnu tělesa (e). Těleso (e) je otevřené. Některé částice mohou být v patřičné hustotní sféře plochou tělesa (e) vytlačeny zpátky do prostředí, kde se tvoří vrstvy s klesající hustotou prostoru, které jsou od sebe oddělené mezifázím (MF 1-2, MF 2-3).

 

2.23.    (a, b, c, e) jsou hmotná tělesa. Na hmotná tělesa (z atomů) můžeme nahlížet jako tělesa fyzikální, nebo tělesa mechanická. [11] Z tohoto pohledu je třeba rozlišovat mechanickou plochu tělesa složeného z atomů (hmotného tělesa) a fyzikální plochu hmotného tělesa (Obr. 7.8.). Mechanická plocha hmotného tělesa, je suma ploch všech atomů, které tvoří povrch tělesa. U mechanické plochy lze v mechanice uplatnit iluzi linearity. Uvnitř (v prostředí) hmotných kapalin a plynů (pevná) mechanická plocha neexistuje. Fyzikální plocha hmotného tělesa je suma ploch všech atomů, těleso tvořících (to znamená i těch uprostřed tělesa). Fyzikální plocha je řádově větší, než plocha mechanická. Fyzikální plocha je vždy sférická.

2.24.    U hmotných těles je třeba rozlišovat fyzikální tlak a mechanický tlak na hmotné těleso působící. Mechanický tlak je tlak jedné mechanické povrchové plochy na jinou mechanickou povrchovou plochu.  Mechanický tlak (odvozený od iluze hmotnosti) lze „vypnout“. Fyzikální tlak je tlak plazmy prostředí (OT) na plochu všech atomů těleso tvořících (na fyzikální plochu tělesa). [12] Fyzikální tlak je důsledkem nehomogenity prostoru a „vypnout“ jej nelze.

2.25.    Povrchová plocha mechanického tělesa (z atomů) působí na jinou mechanickou povrchovou plochu (odstředným) povrchovým tlakem. To je tlak, kterým mechanické těleso „brání“ jiným mechanickým tělesům vniknout dovnitř. Povrchový tlak mechanického tělesa je suma povrchových tlaků atomů tvořících jeho povrch. [13]

2.26.    Povrchový tlak lze definovat jako tlak, který musí vyvinout plocha tělesa (částice) na plochu mezifází, aby se těleso dostalo z jedné hustotní fáze (s jedním tlakem) do vedlejší hustotní fáze (s jiným tlakem). Toto pravidlo platí pro objekty z plazmy (Obr. 7.6.).

2.27.    Je nutno rozlišovat pohyb mechanického tělesa a pohyb fyzikálního tělesa. U pohybu mechanického tělesa (z atomů) na planetě lze uplatnit (na malém území) falešnou iluzi linearity a klidu. Mechanické těleso, které je na planetě s „pevným povrchem“ se může nacházet v „klidu“ vůči vztažné soustavě „pevného povrchu“ planety. Pohyb fyzikálního tělesa je nutno vztahovat vždy k (VSU). To znamená, že fyzikální (dynamické) těleso nikdy není v „klidu“ a vždy se pohybuje (po fraktální spirále).