2. Geometry of space

2.1. Euclidean geometry, Euclidean space

 

2.1.       The fact that we are „small ants“ living on a huge sphere led to the false illusion of a flat Earth. Euclidean geometry, has grown on this illusion, and accompanies us „from cradle to grave“. We cannot imagine that space could be divided or described differently. We believe that Euclidean geometry is universal (applicable throughout the Universe), that it can describe the entire Universe and all phenomena within it. This is a false illusion. [1]

2.2.       „Euclidean space is a virtual (imaginary) space. Euclidean space does not come from natural forces and has no physical properties (unless we „define“ them). It creates the conditions for a false illusion of a kind of neutral place where „theoretical bodies“ exist and „theoretical“ physical events occur. Euclidean space is characterized only by (linear) dimension and allows a false illusion of linearity, homogeneity, symmetry, stillness, and „vacuum“. [2]

2.3.       „Euclidean geometry represents the perception of space based on the idea of a flat Earth. It is characterized by a system of three perpendicular two-dimensional planes intersecting at a single „point.“ The fundamental curve in Euclidean space is a linear line, the fundamental surface is a linear plane, and the fundamental body is a (homogeneous [3] , symmetric, static, closed) cube. Closed (rotating) curves and closed surfaces can exist here. Euclidean (2D) surfaces have no volume.

2.4.       The division of Euclidean space does not stem from natural forces (Figure 2.1. a). Euclidean space is divided based on (virtual) orthogonal linear axes (x, y, z) into identical (virtual) homogeneous, static cubes, depicted in the same gray color. The position and volume of each cube can be precisely determined. Cubes are closed bodies, sharing their (virtual) surfaces, and it’s unclear what separates them from each other. Cubes can be further divided into increasingly smaller, identical, symmetrical, and homogeneous units.

2.5.       In mechanics and the resulting „physics“ working with the false illusion of linear (flat, disconnected) Euclidean space, bodies are separate from space. Space is not considered a (composite) body. The properties of bodies are independent of their position in space. There can be two (or more) bodies with identical, static properties. Bodies are the source of „forces“ that emanate from them throughout their existence (perpetual motion machine). There is absurdity here: empty space = „vacuum“ and an absurd body without volume and surface = „material point“ and others.

 

2.6. Spherical geometry

 

2.6.       Spherical space [4] is a physical (real, material) space. Spherical space is a fractal system of physical densities and physical pressures. Spherical space differentiates only by density - it has no other possibility. The density of space [5] and the pressure (temperature) derived from it in inverse proportion are fundamental physical parameters. The physical density of space is always a positive number. The physical density of space is finite (density floor).

2.7.       In spherical space, it is impossible to find two identical areas, two identical bodies, or two identical trajectories. In spherical space, it is impossible to find two identical or identically repeating events. Spherical space is non-inertial.

 

 

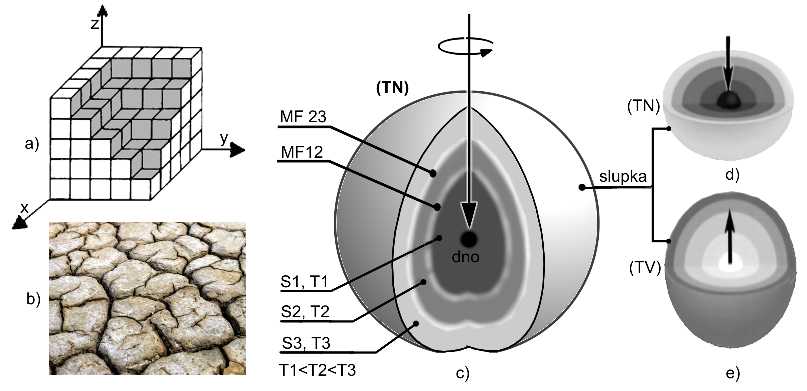
Obr. 2.1.

 

2.8.       The division of spherical space is natural and is created by natural forces. Spherical space consists of a continuous unity of particles with character of high-pressure and low-pressure. In (Figure 2.1. b), the natural division of spherical space can be seen using the example of cracked soil. Areas with a high density of space (soil) are surrounded by areas with a low density of space (atmosphere), and at the same time, areas with a low density of space are surrounded by areas with a high density of space. These natural (fibrous) material structures occur in various forms in all frames of reference in the Universe (Figure 4.2., Figure 4.3.). Dividing such natural spherical structures according to Euclidean rectangular axes or planes is not possible.

2.9.       Spherical space organizes itself according to its density. The process of sedimentation pushes bodies (spatial anomalies) into density spheres (layers) based on their density of space, to which they belong based on their density of space. Through the process of sedimentation, a system of open, non-symmetric layers with increasing or decreasing spatial density is formed in space. In each density layer (sphere), there is a different density of space.

2.10.    The layer (in which bodies have similar physical density of space) is called a phase. Neighboring phases are separated from each other by a physical surface called an interphase (the surface is created by the difference in the density of space). Interphases are not sharp (are „blurry“). The interphase cannot be precisely defined. The greater the difference in space density between two phases, the narrower the interphase between them. The smaller the difference in space density between phases, the wider and less distinct the interphase between them. [6]

2.11.    Inhomogeneous spherical space can have two states. Low pressure (TN) - the density of space increases (pressure decreases) in a spiral towards the center from the shell (Figure 2.1. c, d). High pressure (TV) - the density of space increases (pressure decreases) in a spiral towards the shell from the center (Figure 2.1. e).

2.12.    On (Figure 2.1. c), there is a simplified schematic representation of a spherical space with the characteristic of a low pressure (TN). The density of space increases from the shell towards the center, and the pressure decreases (T1<T2 <T3). The density phases (S1, S2, S3) formed by the sedimentation process are separated from each other by interphases (MF12, MF23...). The center of the low pressure (TN) forms the density bottom (density bottom = dno) of the system. The opposite is true for pressure high (TV).

 

2.13.    „The basic curve (trajectory) in spherical space is a fractal spiral. The fundamental surface in spherical space is a spiral toroid. [7] The fundamental body in spherical space is non-homogeneous, non-symmetric, and dynamic particle. A particle is a physical body bounded by a continuous set of (open) surfaces of spiral toroids. The particle is only a complikated („tangled“) continuous open fractal surface.

2.14.    Fractal spherical geometry of space [8] explains the rules by which space organizes into density spheres and how simple bodies (particles) combine into larger superordinate entities (composite bodies made of particles). It also explains how subordinate pressure systems form in superordinate pressure systems. Due to the fractal nature of space and all the bodies within it, spherical geometry is capable of describing all physical phenomena at all spatial scales, including complex biological systems. It is not a classical geometry with a „ruler and compass.“ Spherical geometry of space lacks any mapping (view) apparatus. When depicting events in spherical space, we must rely on Euclidean geometry.

 

2.15. Relationships between surface and body

 

2.15.    Surface area is a necessary condition for the existence of a body. The surface of a body is a pressure organ. The surface of a body has a centripetal side (d), exerting pressure towards the center of the body, and a centrifugal side (o) exerting pressure away from the center of the body. The pressure from the centrifugal surface of the body is called surface pressure. It is the pressure exerted by the (external) surface of the body on the external surface of another body.

 

 

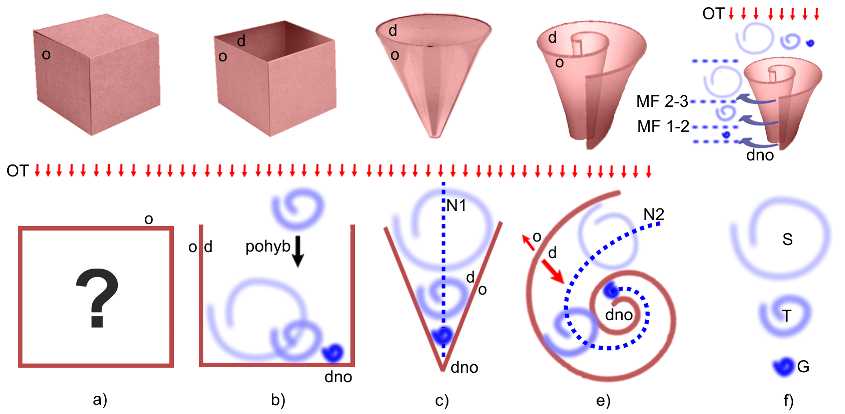
Obr. 2.2.

 

2.16.    Example 2.1. On (Fig. 2.2.), the relationship between several types of (material) bodies (a, b, c, e) and their surfaces is indicated. [9] There are also three „particles“ (S, T, G) with different space densities. Their surface areas (shells) are depicted in a simplified manner as simple open spirals (Fig. 2.2. f).

2.17.    The space density of a particle is determined by the sum of the shell density and the density of what is beneath the inner (centripetal) side of the shell. Particle (S) has a large volume, relatively narrow (dense) shell and a large surface area. The density of space within particle (S) is very small. Inside the particle (S), there is very high pressure (temperature). The particle (T) has a more voluminous shell, a smaller volume of space beneath the shell, and a smaller surface area. Inside the particle (T), the pressure (temperature) is lower than in (S). The density of space in particle (G) is maximal, and the temperature reaches the temperature bottom („zero“ degrees K), its volume is minimal. Nothing denser (colder) can exist in space. [10]

2.18.    The bodies (a, b, c, e) and particles (S, T, G) are situated in an oriented pressure field (OT) acting from „above“ (centripetally). The oriented pressure (OT) pushes on the surfaces of particles (S, T, G), and causes their (centripetal) movement. The bodies (a, b, c, e) differ in their surfaces.

2.19.    The surface of physical body (a) is closed. A closed body has only a centrifugal surface (o). Nothing can be inserted into such a body, nor can anything be taken out of it. Pressure (OT) acts on surface (a) and can cause it to move.  

2.20.    The surface of physical body (b) and (c) can be described as „semi-closed.“ Particles (S, T, G) can be pushed into bodies (b), (c) by pressure (OT), but they cannot escape from the bodies. The pressure (OT) on the (upper) surface of the particles is greater than the pressure (d) from the surfaces of bodies (b) and (c) on the (lower) surface of the particles. The particles (physical bodies) are not a source of any forces and cannot escape from the bodies (b, c) by themself and remaining inside bodies (b, c).  

2.21.    There is a difference in the shape of the surface area between bodies (b) and (c). Body (c) has the shape of a cone (sedimentation cone). The shape of the surface area of body (c) and the pressure (d) from its surface do not allow particles with a large volume (S) to reach the bottom of the cone. Only the densest particles (G) with the smallest volume and surface area reach the bottom of the cone. The centripetal surface of body (c) „sorts“ the particles according to density. In the „axis“ of cone (c), a region of decreasing pressure (N1) is formed.

2.22.    The narrowing spiral surface of body (e) is open. Something can be inserted (pressed) into body (e), and something can also be ejected from it. Particles (S, T, G) are pushed (OT) into body (e). The space density of the particle increases along the spiral (N2) towards the bottom (dno) of body (e). Body (e) is open. Some particles are pushed out from the corresponding density sphere of the body (e) back into the environment, where layers with decreasing density of space are formed, which are separate from each other by interphases (MF 1-2, MF 2-3).  

2.23.    The bodies (a, b, c, e) are mass bodies. Mass bodies (composed of atoms) can be viewed as physical bodies or mechanical bodies. [11] From this perspective, it is necessary to distinguish between the mechanical surface of mass bodies and the physical surface of mass bodies (Fig. 7.8). The mechanical surface of a mass body is the sum of the surfaces of all atoms that make up the mass body's surface. For solid mechanical surfaces, the illusion of linearity can be applied in mechanics. Inside (within the environment) of mass liquids and gases, there is no solid mechanical surface. The physical surface of a mass body is the sum of the surfaces of all atoms that make up the body (including those in the middle of the body). The physical surface is orders of magnitude larger than the mechanical surface. The physical surface is always spherical.

2.24.    It is also necessary to distinguish between physical pressure and mechanical pressure acting on mass bodies. Mechanical pressure is the pressure of one mechanical surface area on another mechanical surface area. Mechanical pressure (derived from the illusion of mechanical weight) can be „turned off“. Physical pressure is the pressure of plasma (OT) on the surface of all atoms forming the body (physical surface). [12] Physical pressure is a consequence of the non-homogeneity of space and cannot be „turned off”.

2.25.    The surface area of one mechanical body (composed of atoms) exerts on the surface area of another mechanical body by (centrifugal) surface pressure. This is the physical pressure by which one mechanical body „defends“ itself to other mechanical body from penetrating inside. The surface pressure of a mechanical body is the sum of the surface pressures of the atoms forming its surface. [13]

2.26.    Surface pressure can also be defined as the physical pressure that the surface of the body (particle) must exert on the interphase surface to transition the body from one density phase (with one pressure) to an adjacent density phase (with a different pressure). This rule also applies to plasma bodies (Fig. 7.6).

2.27.    It is necessary to distinguish between the motion of a mechanical body and the motion of a physical body. In the motion of a mechanical body, a false illusion of linearity (on a small territory) and quiet can be applied. A mechanical body on a planet with a „solid surface“ can appear to be „at quiet“ with respect to the reference frame of the „solid surface“ of the planet. The motion of a physical body must always be related to (VSU). This means that a physical (dynamic) body is never at „quiet“ and always moves along a fractal spiral.